Tree Data Structure
-
A Tree is a non-linear data structure mostly used to represent hierarchical data like a folder structure. A tree node can have zero of more child nodes, but there should be only one parent. So a closed path cannot be created in a tree.
A Tree is an Abstract Data Type that mostly uses Linked List data structure to store data. In most cases, trees require Doubly or Multiple Linked List structure depending on the number of child nodes possible.
Different types of tree structures are there like, binary tree, ordered tree, etc. For tree traversals, we have different algorithms like BFS and uses queues/stacks to record visited nodes.
-
Basic Tree Terminologies
See below some of the basic terminologies used for a Tree Data Structure.
-
Nodes
Each node of a tree are memory allocations to store data and pointers to other nodes. A node can have zero or more child nodes.
-
Root
Only node without a parent node or the starting point of the tree.
-
Edge
Link between nodes. Established as linked lists by storing the address location of child nodes.
-
Degree
Degree of a node is the number of child nodes. Degree of a tree is the maximum number of child nodes available for a node.
-
Size
Size of a tree is the total number of nodes.
-
Height
Height is the number of levels of a tree. A tree with a parent and one or more children in the same level has height 2. If any of the child has another sub-node, height becomes 3.
-
Distance
Number of edges between the shortest path of two nodes.
-
Forest
Forest is a collection of one or more disjoint trees.
-
-
Applications of a Tree
Trees are mostly used to represent hierarchical data. Useful to represent folder structures for computer systems. Used in machine learning software programs like Face Recognition, Natural Language Processing.
Represent XML and HTML document object models. Class hierarchy in Object Oriented Programming. Generate algorithms for many mathematical problems, etc.
-
Types of Tree
Trees are classified into different types according to the number of nodes, type of connections, etc. Let us go through some of the most commonly used Tree structures.
-
Binary Tree
In a Binary Tree, each node can have a maximum of two child nodes. It can be one or zero as well. This is one of the most used types of Tree Data structure and has many applications in search and sort algorithms, design some types of databases, in 3D video games to do the Binary Space Partition to render images, etc.
This is used in certain compression algorithms like Huffman Coding and for cryptography to generate a tree of pseudo random numbers. Morse code is also organized a binary tree.
-
Binary Search Tree
Binary Search Tree is also known as ordered or sorted binary tree. This is a Binary Tree with an additional constraint. Node to the left of the parent has a value lesser than the parent. Node values to the right is always greater than the parent value.
Binary Search Trees are used in sorting algorithms like Tree Sort and Quick Sort and also to implement Priority Queues.
-
Balanced Tree
Balanced Tree or a Self Balancing Binary Search Tree is a type of Binary Search Tree that automatically rearranges itself when an insert or delete happens. Re-arrangement is done in such a way that the height is always minimum. This results in a tree structure that is more spread out (breadth-wise) rather than just increasing the tree height.
Self balancing trees allows fast traversal of items in the key order. Can be used to construct and maintain ordered lists like priority queues and can be used to implement any algorithm that uses ordered lists or priority queues to achieve optimal Time Complexity performance. Self balancing trees are less efficient for sorting algorithms.
Different types of balanced trees are available. Below we will see 2 of those; B-Tree and AVL Tree.
-
B-Tree
B-Tree maintains data in sorted order for fast search, traversal and insert/delete operations. Usually these operations can be performed on logarithmic time complexity.
This feature makes B-Tree much suited to for databases and file systems. B-Tree based indexing speeds up search operations.
-
AVL Tree
AVL Tree is a type Self Balancing Tree. Constraint is that the height of two child sub trees always differ by a maximum of 1. Of it becomes more that one, re-arrangement happens. Than means, when a node is inserted or deleted, height of all parent nodes are checked and if the above condition is not satisfied, all or some of the nodes are re-arranged.
AVL Trees are of less usage in real-world scenarios. These are useful in indexing larger tables of data, in-memory sorts of lists and dictionaries although easier alternatives are now available.
-
-
Trie
Trie is a type of tree structure that handles strings mostly. Tries are used to design auto-completes or spell checkers to generate suggestions.
For example to design a dictionary, second level after root can have 26 sub-nodes. Then each of these nodes has sub-levels that corresponds to any word available in the dictionary. So when we type a character, algorithms can easily navigate through the sub-nodes to suggest the possible words. Final node for each node should also have some marker to represent end of the word.
Tries perform extremely fast for auto-completes or spell checkers, but size may become very high.
-
-
Tree Traversals
We have three ways to navigate through the Tree based Data Structures. These are In Order, Pre Order and Post Order. A tree has basically a root node and some child nodes to the left and some to the right. The mentioned classifications are the order in which each of these nodes are traversed.
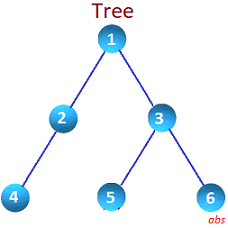
Consider below tree to easily understand the concept.
-
In-Order
Left most nodes are accessed first. Then middle and then right. Output of the above tree structure will be 4, 2, 1, 5, 3, 6.
-
Pre-Order
Root is traversed first, then left and then right. Output will be 1, 2, 4, 3, 5, 6.
-
Post-Order
First, left most nodes are accessed, then right and finally middle nodes. Output will be 4, 2, 1, 5, 6, 3.
-
-
Tree Based Algorithms
The basic tasks that are performed on a tree are traversals, search, insert/update/delete and sort. Sorting is basically re-arranging nodes of the Binary Search Trees after an insert, update or delete action.
There are many algorithms to do the above tasks depending on the type of the trees. We will see these in detail in the upcoming modules.
