Exponential Search

Exponential Search, like Binary Search is used to find an element from a sorted list. Other names of this type of search are doubling search or galloping search or Struzik search. Exponential Search works in two parts. First part finds a range within the list, which could have the searched item. Second part performs a Binary Search within the range to check for the searched item.

Exponential Search has better performance than Linear Search. This can also perform better than Binary Search, when the element being searched are closer to the start of the array. This is because, the range is shorter at the beginning and also because the first part of the search, finishes execution in less iterations.

If searched items are near the end of the list, performance is lesser than Binary Search.

Time complexity of Exponential Search for average and worst cases are represented as O_{(log i)}, i being the index of the searched item. Space complexity is O₍₁₎.

Practical use cases of Exponential Search are limited as Binary Search perform better in most of the scenarios.
How Exponential Search Works

Exponential Search is also a divide and conquer method. Exponential search works in two parts similar to Jump Search.

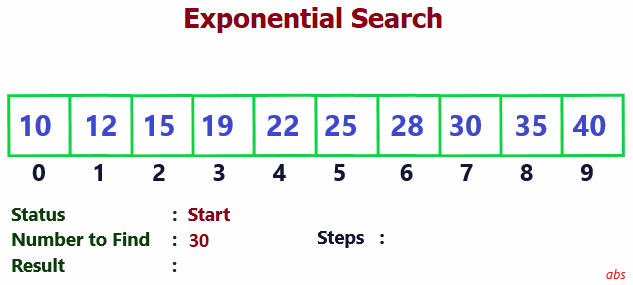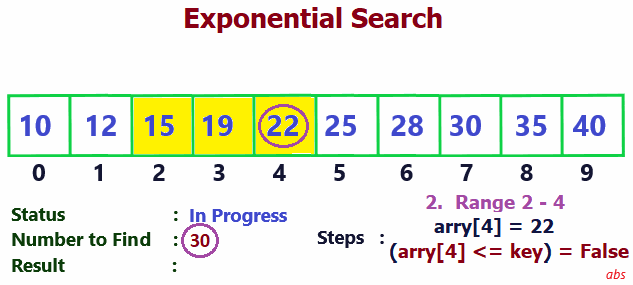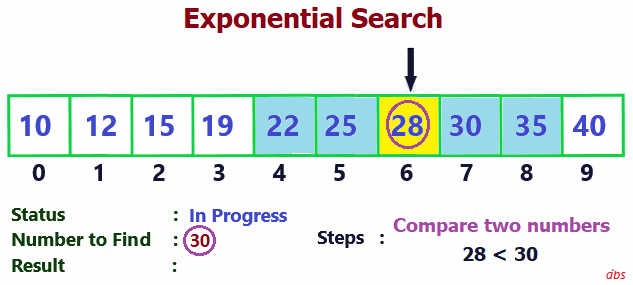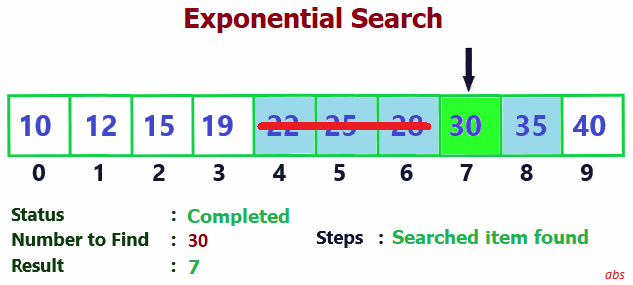
First section identifies a range within the array. If the searched item is present in the array, it will be within this range only. This is done by comparing the search key and the last element of each range.

Once the range is identified, a Binary Search is performed on this range to check if the item is present.

In the basic form of Exponential Search, start and end of the range are identified as the power of 2. For example;
- Range 1 : Start = 0, End = 1
- Range 2 : Start = 2¹ = 2, End = 2² = 4
- Range 3 : Start = 2² = 4, End = 2³ = 8
- Range 4 : Start = 2³ = 8, End = 2⁴ = 16
- Range 5 : Start = 2⁴ = 16, End = 2⁵ = 32
Check the below gif image to easily understand the search process.
Algorithm

Exponential Search Algorithm flow is listed as below.

Input : A sorted list of elements.
Output : Element position, if found. Else not found message.
1. Start.
2. Set start = 0, end = 1, pos = -1.
  start and end values represents the first range.
3. Check if the searched item can be present within this range using formula arry[end] <= searched item
4. If True, range identified. Exit loop. Go to step 6.
5. If False, find next range. Start = Previous end, End = Start * 2. Go to step 3.
6. Perform Binary Search on the identified range and check for the element and return the pos.
7. If pos > -1, element found. Display result.
8. Else if pos = -1, element not found. Display not found message.
9. Stop.

Code Samples

Below are few sample code implementations of Exponential Search Algorithm in Python, Java, C# and JavaScript.

def BinarySearch(arry, start, end, find):
    pos = -1
    while (start <= end):
        midNode = int( (start + end) // 2 )
        if (arry[midNode] == find):
            pos = midNode
            break

        if (arry[midNode] < find):
            start = midNode + 1
        else:
            end = midNode - 1
    return pos


arry = [10, 12, 15, 19, 22, 25, 28, 30, 35, 40]
find = 35
pos = -1
arrLen = len(arry)

if (arry[0] == find):
    pos = 0

bound = 1
while (bound < arrLen and arry[bound] <= find):
    bound = bound * 2
pos = BinarySearch(arry, bound / 2, min(bound, arrLen - 1), find)

if(pos > -1):
    print("Element found at position : ", pos)
else:
    print("Element not found")

class ExponentialSearch   
{
    public static void main(String[] args)   
    {  
        int arry[] = {10, 12, 15, 19, 22, 25, 28, 30, 35, 40};
        int find = 35;
        int pos = -1;
        int arrLen = arry.length;

        if (arry[0] == find)
            pos = 0;

        int bound = 1;
        while (bound < arrLen && arry[bound] <= find)
            bound = bound * 2;

        pos = BinarySearch(arry, bound / 2, Math.min(bound, arrLen - 1), find);

        if (pos > -1)
            System.out.println("Element found at position : " + pos);
        else
            System.out.println("Element not found");
    }

    static int BinarySearch(int[] arry, int start, int end, int find)
    {
        int pos = -1;
        while (start <= end)
        {
            int midNode = (start + end) / 2;
            if (arry[midNode] == find)
            {
                pos = midNode;
                break;
            }

            if (arry[midNode] < find)
                start = midNode + 1;
            else
                end = midNode - 1;
        }

        return pos;
    }
}

using System;
using System.Threading;

namespace DSA
{
    class Program
    {
        static void Main(string[] args)
        {
            int[] arry = { 10, 12, 15, 19, 22, 25, 28, 30, 35, 40 };
            int find = 35;
            int pos = -1;
            int arrLen = arry.Length;

            if (arry[0] == find)
                pos = 0;

            int bound = 1;
            while (bound < arrLen && arry[bound] <= find)
                bound = bound * 2;

            pos = BinarySearch(arry, bound / 2, Math.Min(bound, arrLen - 1), find);

            if (pos > -1)
                Console.Write("Element found at position : " + pos);
            else
                Console.Write("Element not found");

            Thread.Sleep(5000);
        }

        static int BinarySearch(int[] arry, int start, int end, int find)
        {
            int pos = -1;
            while (start <= end)
            {
                int midNode = (start + end) / 2;
                if (arry[midNode] == find)
                {
                    pos = midNode;
                    break;
                }

                if (arry[midNode] < find)
                    start = midNode + 1;
                else
                    end = midNode - 1;
            }

            return pos;
        }
    }
}

function exponentialSearch(find) {
    var arry = [ 10, 12, 15, 19, 22, 25, 28, 30, 35, 40 ];
    var find = 35;
    var pos = -1;
    var arrLen = arry.length;

    if (arry[0] == find)
        pos = 0;

    var bound = 1;
    while (bound < arrLen && arry[bound] <= find)
        bound = bound * 2;
    
    pos = binarySearch(arry, bound / 2, Math.min(bound, arrLen - 1), find);

    if (pos > -1)
        alert("Element found at position : " + pos);
    else
        alert("Element not found");
    return false;
}

function binarySearch(arry, start, end, find) {
    
    var pos = -1;
    while (start <= end)
    {
        var midNode = Math.floor((start + end) / 2);
        if (arry[midNode] == find)
        {
            pos = midNode;
            break;
        }

        if (arry[midNode] < find)
            start = midNode + 1;
        else
            end = midNode - 1;
    }

    return pos;
}

var find = 35;
exponentialSearch(find);

Exponential Search

How Exponential Search Works

Algorithm

Code Samples