Stack Data Structure

Stack can be considered as a version of array that can be used to dynamically add or remove elements. Stack data structures are implemented based on LIFO principle. That means the elements are added in such a way that the first element entered to a stack can only be removed last.

Queues and Stacks can be used as a buffer to keep some data for later processing and is an important part of the Backtracking concept, which forms the code of most algorithms of data structures.

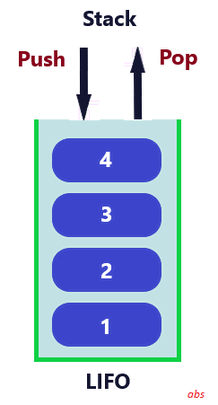
Stack is also an Abstract Data Type (ADT), since these are modified versions of either Linked List or Array data structures. To these data structures, if we just add two more functionalities (methods), it becomes a Stack. First is a push() method that inserts elements to the top of the Stack. Second is a pop() method to remove elements from the top itself.

Another common method that most Stack implementations have is a peek() method, that fetches the top element without actually removing it.

Let us see how we can convert an Array or Linked List to Stack. We will use Java because, Java has built-in Array and Linked List data structures.

Stack implementation using Array Data Structure

Let us see how we can make a Stack out of an Array. We are going to add 3 functionalities to insert remove and peek.

Difference with the Queue is in pop() and peek() methods. Rather that removing item at zero position, n-1^th item is removed or peeked. Also Stack implementation of pop() doesn't need a re-arrangement.

class Stack   
{
    private int itemsCount;
    private int[] arry;
    
    Stack(int size)  
    {
        this.itemsCount = 0;
        this.arry = new int[size];
    }  
  
    public void push(int num)  
    {
        if(itemsCount < arry.length) {
            arry[itemsCount] = num;
            itemsCount++;
            System.out.println(num + ", added to stack");
        }
        else {
            System.out.println("Max size reached");
        }
    }

    public int pop()
    {
        int popItem = -1;
        if(itemsCount > 0) {
            popItem = arry[itemsCount-1];
            itemsCount--;
        }
        return popItem;
    }

    public void peek()  
    {
        if(itemsCount > 0) {
            System.out.println("Top item : " + arry[itemsCount-1]);
        }
        else {
            System.out.println("Stack is empty");
        }
    }
    public static void main(String[] args)   
    {  
        Stack q = new Stack(5);
        q.push(1);
        q.push(2);
        q.push(3);
        System.out.println(q.pop() + ", removed from stack");
        System.out.println(q.pop() + ", removed from stack");
        q.peek();
        System.out.println(q.pop() + ", removed from stack");
        q.peek();
        q.push(4);
        q.push(5);
        q.peek();
        q.push(6);
        q.push(7);
  }  
}

Output: 1, added to stack 2, added to stack 3, added to stack 3, removed from stack 2, removed from stack Top item : 1 1, removed from stack Stack is empty 4, added to stack 5, added to stack Top item : 5 6, added to stack 7, added to stack

Stack implementation using Linked List Data Structure

Java has a built-in LinkedList data structure within java.util.LinkedList namespace. And there are built-in methods as well to make the LinkedList work like a Stack.

Use push() method to insert data to the top of the Stack.

Use pop() method to remove and return the top element.

Use peek() to check the top element, without removing it.

import java.util.LinkedList;

class Stack   
{
    public static void main(String[] args)   
    {  
        LinkedList<Integer> ll = new LinkedList<Integer>();

        ll.push(1);
        ll.push(2);
        ll.push(3);
        System.out.println(ll.pop() + ", removed from stack");
        System.out.println(ll);
        System.out.println(ll.peek());
        ll.push(4);
        System.out.println(ll);
        System.out.println(ll.peek());
  }  
}

Output: 3, removed from stack [2, 1] 2 [4, 2, 1] 4

Uses of a Stack

Stacks forms the basis of Backtracking and many algorithms like Depth First Search (DFS) uses stacks to store elements for next iterations.

Algorithms like Graham scan, SMAWK nearest-neighbor chain uses stacks.

Many Programming Languages uses stacks to perform arithmetic operations (to store numbers).

Stack Data Structure

Stack implementation using Array Data Structure

Stack implementation using Linked List Data Structure

Uses of a Stack