Interpolation Search

Interpolation Search can be considered as an improved version of Binary Search. Like Binary Search, Interpolation Search is used to find an element from a sorted list. In certain scenarios, Interpolation Search works better than Binary Search. This type of search works best, if the array contains numerical values only.

Difference between Interpolation Search and Binary Search is that each iteration of Binary Search always chooses the middle of the remaining search space and discards a half of the remaining items. But in Interpolation Search, instead of finding a middle node, a probe node is identified using Linear Interpolation mathematical method.

Below is the formula used to find the Probe Node. As you can see, this is most suited for array of numbers. If the array contains non-numeric values, modification is needed for the formula. Check the gif image below for better understanding.

probe = start + ( ( (key - arry[start]) * (end - start) ) / (arry[end] - arry[start]) )

The idea is that the probe node identified should be much closer to the searched item in most cases and so it is able to discard more items in one iteration. So the number of iterations required is less compared to Binary Search.

The code samples provided in this page and the Binary Search page uses the same array. But, you can see that the Interpolation Search finds the searched item in 1 or 2 iterations, whereas Binary Search requires 3 or 4 iterations for most numbers in the list.

Time complexity of Interpolation Search for average case O_{(log(log(n)))} and for worst case is O_(n). Space complexity is O₍₁₎.

Interpolation Search Uses

Interpolation search works better than Binary Search if the elements in the array are uniformly distributed. There are many practical use cases of Interpolation Search like predicting the price of a Share by going through the past prices. Interpolation techniques are used in Natural Language Processing and Image Processing algorithms.
How Interpolation Search Works

Interpolation Search is also a divide and conquer method. In Interpolation Search, instead of finding a middle node, a Probe Node is identified using Linear Interpolation mathematical method using the below formula.

probe = start + ( ( (key - arry[start]) * (end - start) ) / (arry[end] - arry[start]) )

Then like, Binary Search, this Probe Node is compared with the searched element and discards a part of the array till the result is obtained.

Check the below gif image to easily understand the search process.
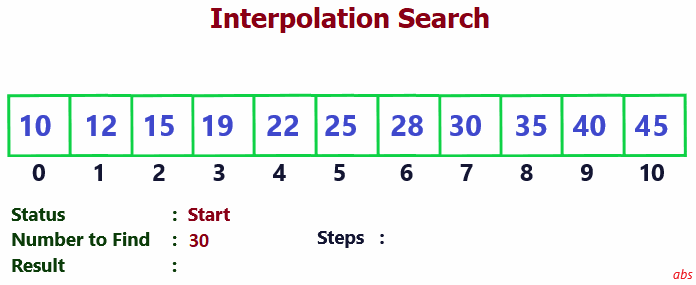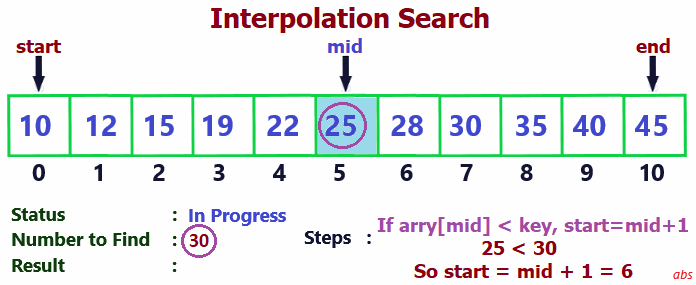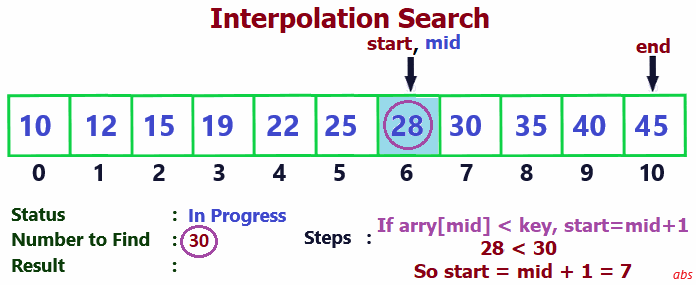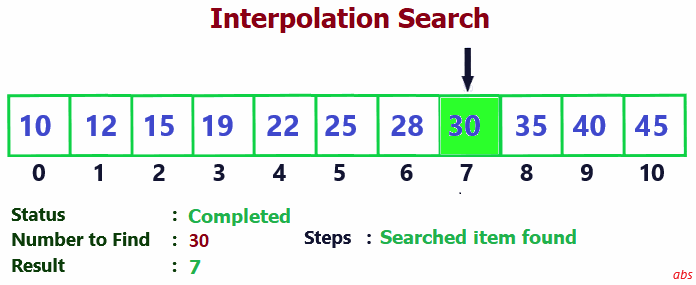
Algorithm

Interpolation Search Algorithm flow is listed as below.

Input : A sorted list of elements.
Output : Element position, if found. Else not found message.
1. Start.
2. Set start = 0, end = length of array, pos = -1.
3. Check key between start and end, if true go to next step, else go to step 8.
4. Find probe node.
5. If probe node value = searched value, element found. Go to step 8.
6. Else if probe node value < searched value, set start = probe node + 1. Go to step 4.
7. Else, end = probe node - 1. Go to step 4.
8. If pos > -1, element found. Display result.
9. Else if pos = -1, element not found. Display not found message.
10. Stop.

Code Samples

Below are few sample code implementations of Interpolation Search Algorithm in Python, Java, C# and JavaScript.

import math

arry = [10, 12, 15, 19, 22, 25, 28, 30, 35, 40]
find = 35
pos = -1
count = 0

start = 0
end = len(arry) - 1
midNode = 0

#Check algorithm section if any clarification needed in the logic
while ((arry[end] != arry[start]) and (find >= arry[start]) and (find <= arry[end])):
    count += 1
    midNode = start + int((find - arry[start]) * (end - start) / (arry[end] - arry[start]))

    if (arry[midNode] < find):
        start = midNode + 1
    elif (find < arry[midNode]):
        end = midNode - 1
    else:
        pos = midNode
        break

if (find == arry[start]):
    pos = start

if(pos > -1):
    print("Element found at position : ", pos)
else:
    print("Element not found")

print("Number of Iterations : ", count)

class InterpolationSearch   
{
    public static void main(String[] args)   
    {  
        int arry[] = {10, 12, 15, 19, 22, 25, 28, 30, 35, 40};
        int find = 35;
        int pos = -1;
        int count = 0;

        int start = 0;
        int end = arry.length - 1;
        int midNode = 0;

        //Check algorithm section if any clarification needed in the logic
        while ((arry[end] != arry[start]) && (find >= arry[start]) && (find <= arry[end]))
        {
            count += 1;
            midNode = start + ((find - arry[start]) * (end - start) / (arry[end] - arry[start]));

            if (arry[midNode] < find)
                start = midNode + 1;
            else if (find < arry[midNode])
                end = midNode - 1;
            else
            {
                pos = midNode;
                break;
            }
        }

        if (find == arry[start])
            pos = start;

        if (pos > -1)
            System.out.println("Element found at position : " + pos);
        else
            System.out.println("Element not found");

        System.out.println("Number of Iterations : " + count);
    }
}

using System;
using System.Threading;

namespace DSA
{
   class Program
   {
       static void Main(string[] args)
       {
           int[] arry = { 10, 12, 15, 19, 22, 25, 28, 30, 35, 40, 45 };
           int find = 30;
           int pos = -1;
           int count = 0;

           int start = 0;
           int end = arry.Length - 1;
           int midNode = 0;

           //Check algorithm section if any clarification needed in the logic
           while ((arry[end] != arry[start]) && (find >= arry[start]) && (find <= arry[end]))
           {
               count += 1;
               midNode = start + ((find - arry[start]) * (end - start) / (arry[end] - arry[start]));

               if (arry[midNode] < find)
                   start = midNode + 1;
               else if (find < arry[midNode])
                   end = midNode - 1;
               else
               {
                   pos = midNode;
                   break;
               }
           }

           if (find == arry[start])
               pos = start;

           if (pos > -1)
               Console.Write("Element found at position : " + pos);
           else
               Console.Write("Element not found");

           Console.WriteLine("\r\nNumber of Iterations : " + count);
           Thread.Sleep(5000);
       }
   }
}

function interpolationSearch(find) {
    var arry = [ 10, 12, 15, 19, 22, 25, 28, 30, 35, 40 ];
    var find = 35;
    var pos = -1;
    var count = 0;

    var start = 0;
    var end = arry.length - 1;
    var midNode = 0;
    
    //Check algorithm section if any clarification needed in the logic
    while ((arry[end] != arry[start]) && (find >= arry[start]) && (find <= arry[end])) {
        count += 1;
        midNode = start + Math.floor((find - arry[start]) * (end - start) / (arry[end] - arry[start]));

        if (arry[midNode] < find)
            start = midNode + 1;
        else if (find < arry[midNode])
            end = midNode - 1;
        else {
            pos = midNode;
            break;
        }
    }

    if (find == arry[start])
        pos = start;

    if (pos > -1)
        alert("Element found at position : " + pos);
    else
        alert("Element not found");

    alert("Number of Iterations : " + count);
    return false;
}

var find = 35;
interpolationSearch(find);

Interpolation Search

Interpolation Search Uses

How Interpolation Search Works

Algorithm

Code Samples