Divide and Conquer Algorithms
-
Divide and Conquer Algorithms are a type of algorithm design that effectively splits input data structures into multiple sub-units and looking for answer in each sub-unit. If needed the sub-units are re-arranged and re-combined.
These types of algorithms are implemented using recursion. We can avoid recursive function calls and replace it with loops as well.
-
A quick comparison
Let us do a quick comparison of Linear Search and Binary Search algorithms. Linear Search uses sequential search and Binary Search uses Divide and Conquer Method.
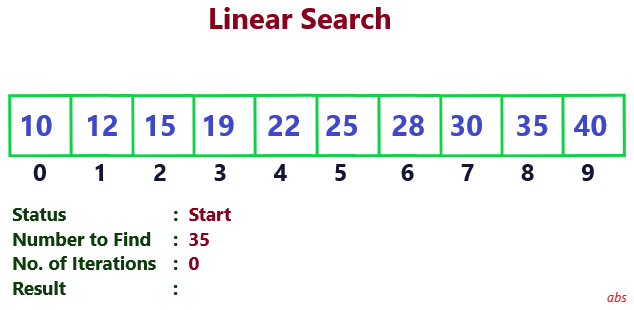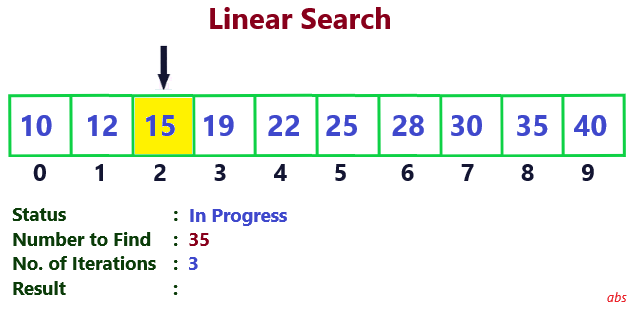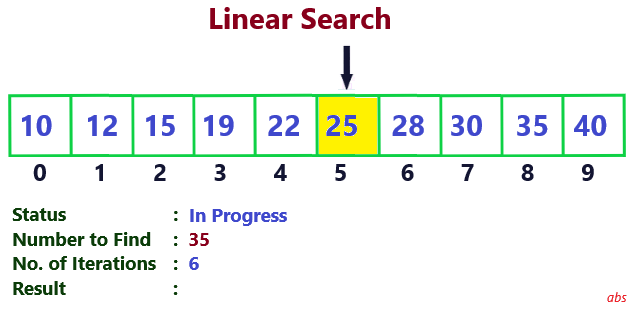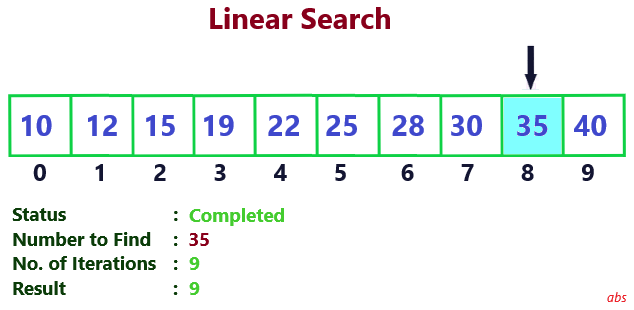
In this example, we are going to search for number 35 in a sorted array of 10 numbers.
Linear Search
Nodes are searched sequentially till the searched number is found. 9 iterations are required. So time complexity is 9.
Binary Search
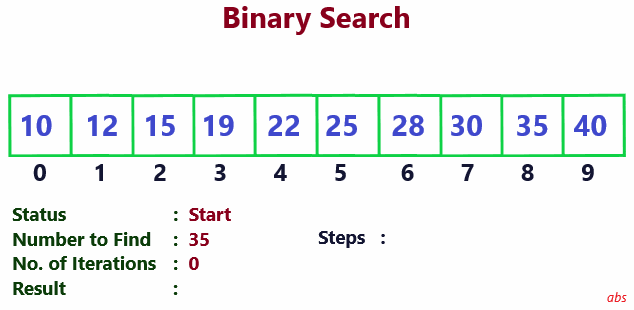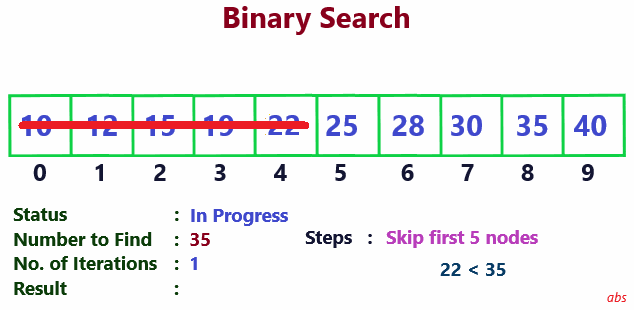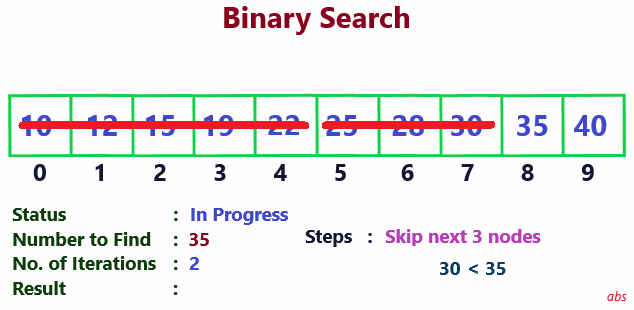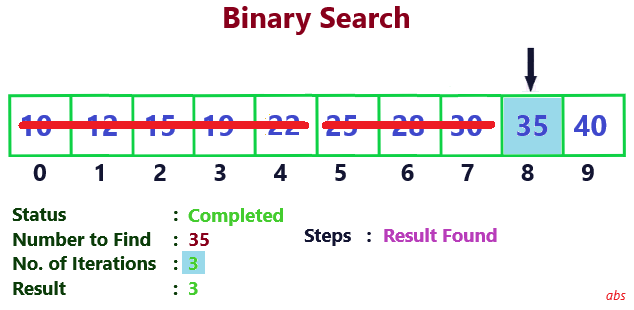
For each iteration, middle node of the array is found. Compare the value of this node with the searched number. If both are equal, it is the result. If middle node value is less than searched number, skip the first half for next iteration. Otherwise skip the second half. Continue this till the searched number is found.
For this example, result is found in 3 iterations. You can try different options and can find that average and worst case time complexity is always better for divide and conquer approach.
The dark green line in the above graph is a logarithmic path. As you can see this is well below the Linear Time Complexity line.
This is because, divide and conquer method eliminates a section of nodes after each iteration, there by reducing the number of iterations required making the average and worst case scenarios perform much better.
-
Why use Divide and Conquer Algorithms
Such type of algorithms perform much better compared to normal algorithms in terms of Time complexity. These algorithms follow a logarithmic path in Time Complexity Graph. This means that efficiency increases as the number of inputs increases, making it very effective for data structures with huge amount of data.
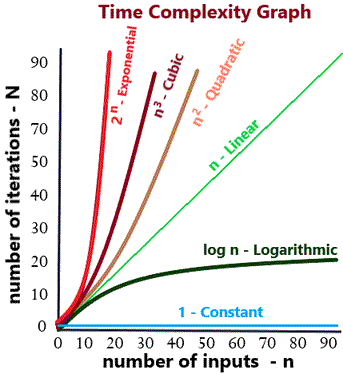
The dark green line in the above graph is a logarithmic path. As you can see this is well below the Linear Time Complexity line.
This is because, divide and conquer method eliminates a section of nodes after each iteration, there by reducing the number of iterations required making the average and worst case scenarios perform much better.
-
Advantages
Divide and conquer method gives better performance for sort and search functionalities. Fastest sorting algorithms Merge Sort, Heap Sort and Quick Sort uses this method.
Search algorithms like Binary Search, Interpolation Search, Exponential Search and Fibonacci Search use different approaches to divide the data and provides better performances compared to other approaches.
Useful in solving various types of puzzles like Tower of Hanoi, arithmetic operations like multiplication of larger numbers, Discrete Fourier Transform, etc. Used in shortest path finding algorithms as well.
-
Approaches
Different types of approaches are used by different divide and conquer algorithms. Some details below.
Binary Search divides array of nodes to half for each iteration, eliminating one half after each.
Exponential Search first finds a range of nodes to search for and eliminates the rest, then binary search is applied on the remaining nodes.
Fibonacci Search splits the array to the lengths of two consecutive Fibonacci numbers, take one part for next iteration and eliminating next part of the array.
Merge Sort splits the array into n number of sub-arrays (n is the length of the array). Then each item is merged back, in-order to get the sorted array.
Heap Sort divides array into sorted and unsorted sub-arrays. Then it fetches the largest element from unsorted arrays and inserts into the sorted ones and then combine all the sorted arrays.
Quick Sort works by splitting arrays to two based on a pivot element and then does the recursive sorting of sub-arrays.
